Noodlings

This has come up a couple times in the past couple months leading me to believe that there are others out there who might benefit from this. I’m overdue for an post anyways.

The question: How do you draw shapes with holes in them? (i.e. How do I draw a donut?)

Short answer: Winding rules.

So what’s a winding rule? A winding rule is a way to determine whether a point is inside or outside a shape, useful for when you want to fill a shape. Quartz (like Postscript) has two different winding rules: even-odd and non-zero.

Non-zero is the default. How does it work? Take the point in question. Follow a line from that point extending out to infinity. Now, maintain a count. Increment the count every time you cross the path with the path going from left to right. Decrement whenever you cross a path going from right to left. In the end, if the count is zero, you are outside the shape, otherwise you are inside.

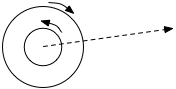
In the diagram above, the final count is zero. Note that this is a compound path (remember, paths do not have to be contiguous). Our imaginary ray crosses the path twice but does so with the paths going in opposite directions. This means that the point in the middle of both circles is considered outside the shape. Voilà , a donut.

With even-odd, it’s a bit simpler. Draw a line out from the point but just increment every time you cross the path (regardless of direction). If the resulting count is even, you are outside, otherwise you are inside.

Except for the labels on the axes, the pic below is actual output from a Cocoa program showing different combinations. The top two shapes have the outer and inner circles specified going in the same direction. The bottom two have the inner cirlce going in the opposite direction as the outer. The shapes on the left are drawn with non-zero winding while the two on the right are drawn with even-odd. Paths are stroked in white.

Notice how the direction of the paths does not matter for even-odd. Also notice how in the case of non-zero with the paths going in the same direction (top-left donut), the inner circle is considered a part of the shape’s interior. This shows that non-zero gives you more control (you can control what parts of the shape are considered inside by adjusting the direction of the paths). It is also more tedious to deal with for the more simple cases. To draw donuts using non-zero, I did the outer circle, created another path for the inner circle, reversed it and added it to the outer circle’s path. Using even-odd, all I had to do is set the winding rule on the path. For more complex cases, the control of non-zero winding may be required but for simple shapes like donuts, use even-odd. Why you’d ever want to draw anything else besides donuts is beyond me; donuts are delicious. While this knowledge can be applied to other less worthy shapes, I cannot be held responsible for the jeers you will undoubtedly receive for even daring to allow to cross one’s mind the slightest notion of contemplating considering drawing anything non-donut-like.

I’m too lazy busy to clean up the code for you to download but play with it yourself. It can all be done via NSBezierPath (key methods are -bezierPathByReversingPath and -setWindingRule:). Also, the winding rules can apply to clipping as indicated by the following pic:

For extra credit, play with self-intersecting paths.

Enjoy.